The Equation That Outsmarts AI: y=mx+b

gpt-4o gets it wrong 50% of the time. What are these math benchmarks proving?

GPT-4o cannot reliably calculate a linear equation.

Key Findings:

1. Your prompt and temperature settings matter

2. LLMs are good at pretty numbers like 10, 20, 100, 200, etc…

3. GPT-4o gets y=mx+b wrong 50% of the time for “large” numbers (>1000)

4. The same limitations exist for all current LLMs, any improvement in benchmarks is simply a better training set that includes the benchmarks problems, rather than an increase in reasoning or capability.

5. Oddly, performance on MATH benchmark does not correlate to y=mx+b performance.

A few months ago while working on a contract for a large education company, I came across a problem with ChatGPT - it couldn’t solve y=mx+b for even basic numbers.

Now I know LLMs are Language Models but time and time again I see them crushing at certain math benchmarks. The big one you will see touted frequently is the “MATH” benchmark (which isn’t an acronym btw).

MATH, as stated by their website is

The test consists of 12,500 problems from high school math competitions.

The test is hard and the researchers introducing the dataset found that a PhD student who does not especially like mathematics scored 40%, and a three-time IMO gold medalist got 90%.

And their most recent charts show LLMs like GPT-4o getting impressive scores!

Nearly 80% by GPT-4o, neat!

The formula I was working on was a simple linear equation, and after some prompting, I realized that if I had it explain its work, it got the answer correct. For example, prompting with “You are a math assistant; please return your answer as y = [number]” will give you an accuracy of only 20% or less. Instead, prompting it to “show your work” will increase accuracy dramatically.

Digging In

But surely, prompting cannot explain everything. Even with a good prompt, it was still inconsistent. Immediately, I turned to the temperature setting, as that seemed to cause it to sometimes get answers correct and other times get answers wrong.

With the temperature set to 0, I was now getting y=mx+b correct for any number under 100 easily.

Growing Up

However, knowing that LLMs aren’t actually reasoning or calculating, how far can they go with math?

To scale up this experiment, I created a script that went from 0 to 10,000, incrementing m, x, and b by 11. Why 11? For one, I didn’t want to run an LLM that costs money 10,000 times, and if you use a neat increment, like 10, it actually gets the answer correct more often.

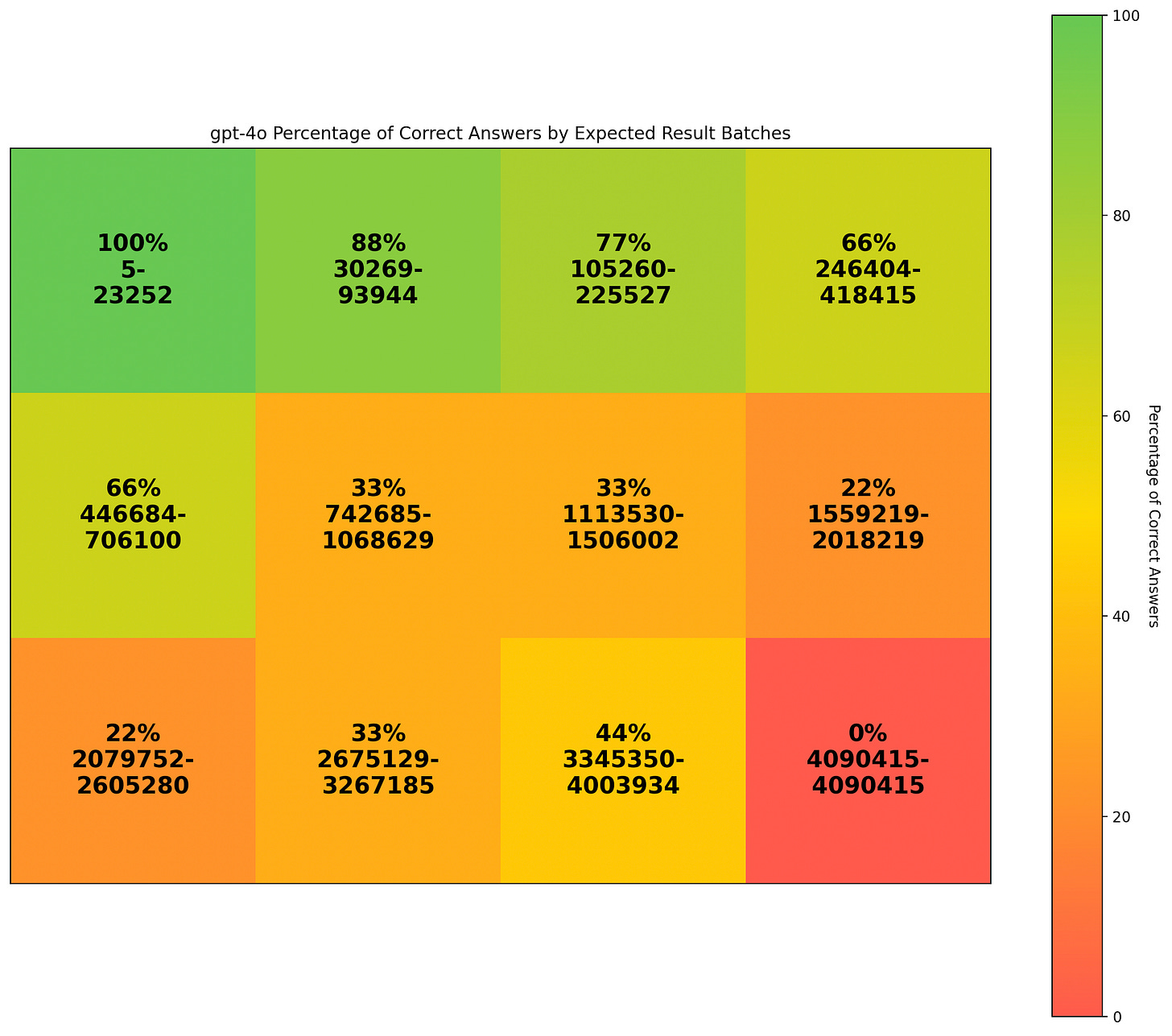
Unfortunately, this is a linear equation, so plotting it just creates a line chart. Instead, let’s pivot the data into a grid, grouping by what the result of y=mx+b should have been, and then analyze the percentage of accurate calculations. This captures how LLM’s struggle with larger numbers.

As you can see, GPT-4o gets smaller numbers correct, but is struggling almost immediately, the first failure coming at just m=232, x=254 and b=276 and it only gets worse from there.

I ended running until m=3200 because it didn’t make sense to see if it magically started being 100% correct again.

What About Second Model?

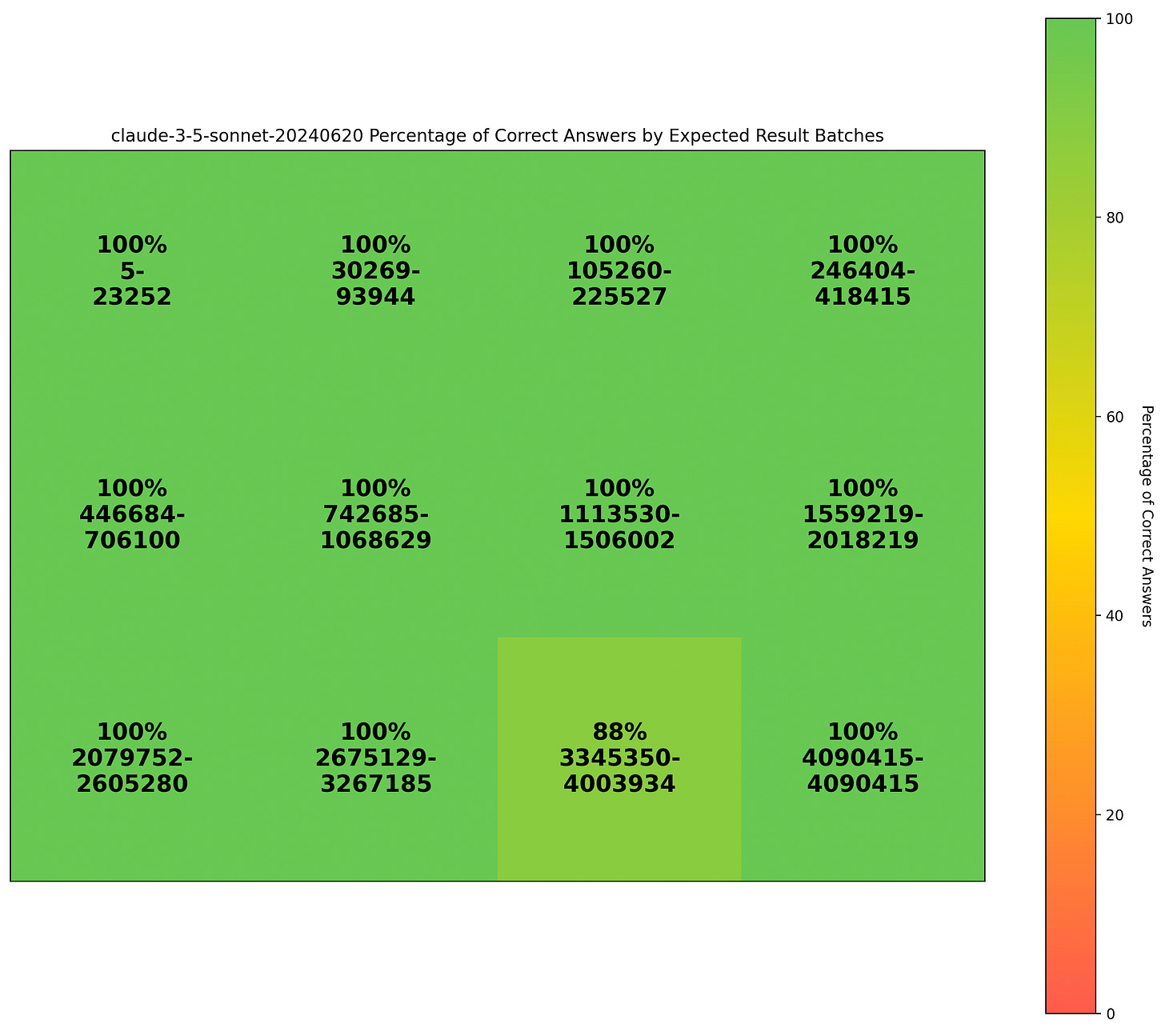
Let’s try with Claude 3.5 Sonnet

Much better than gpt-4o. I ran it until it reached ~3000 on this first run just to see if it replicated the same issue. Claude shows dramatically better performance, with only a couple odd failures.

The Final Frontier

Using this script, we can actually find how far a model can go before falling below 50% accuracy. To speed things up a bit, I ran this batch in increments of 101 and found that Claude starts to fall off shortly after my last test, around x and m > 4000.

At this point, Claude 3.5 is wrong more than half the time, I actually validated this up to m, x = 10000 and it remains around 20-40%.

Why Does This Happen?

Simply put, it’s because of tokens (imagine doing math 2 numbers at a time), small working memory and single pass architecture.

From: https://arxiv.org/html/2407.11373v1

1. Models are expected to generate an answer in a single pass of their feedforward architecture, which cannot implement conditional loops

2. Moreover, the statistical nature of LLMs’ training and representation means they often fail in generalizing appropriately to problems outside their training distribution, especially in settings requiring reasoning and discrete processes

3. Furthermore, even the most advanced LLMs, including GPT4, have an incredibly short working memory[4], while reliable reasoning requires accurate and robust retrieval and integration of all relevant information.

How Should I use an LLM for Math in Education?

Very carefully. I highly recommend not using them for any complex math reasoning, or if you are going to make sure you guide the LLM closely. Chain of Thought is about the only way to make it do a good job, or use another LLM to validate your output. Also carefully bench marking your LLMs is definitely a NEED (as always).

A New Benchmark?

Honestly, I was surprised to see that they mainly benchmark LLMs with word problems. Obviously that is a great way to show its proficiency in *language* but is that really the best way to show their math capabilities?